O-notation: Analysis of algorithm complexity

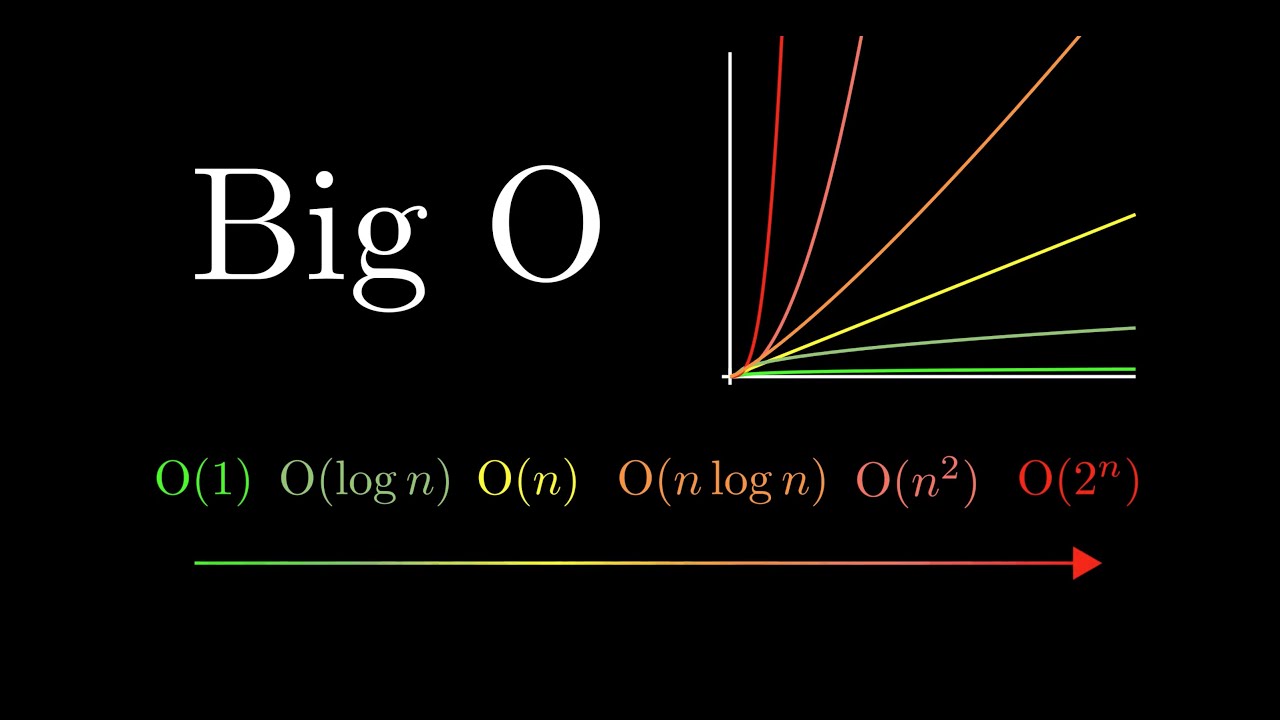
Fundamentals of O-Notation: An introduction to algorithm analysis

O-notation, also known as Landau notation or Big-O notation, is an important concept in computer science and software development that is used to analyze the runtime complexity of algorithms. This notation enables developers and computer scientists to objectively evaluate and compare the performance and efficiency of algorithms. At its core, the O-notation helps to understand how the runtime of an algorithm behaves in relation to the size of the input data. It makes it possible to make predictions about how an algorithm will react to larger amounts of data. This is crucial to ensure that software works efficiently in practice and completes the desired tasks in an acceptable amount of time. O-notation uses mathematical symbols such as "O", "Ω" and "Θ" to describe different aspects of runtime complexity. "O" represents the upper bound, "Ω" the lower bound and "Θ" the exact bound. However, the analysis usually focuses on the upper bound, as developers are often interested in understanding the worst-case scenario. A common example is the O(1) complexity, which indicates that the runtime of an algorithm is constant, regardless of the input size. In contrast, the O(n) complexity indicates that the runtime grows linearly with the size of the input. Mastering O-notation is invaluable for software developers, as it provides a sound basis for decision-making when selecting and optimizing algorithms. In further subtitles, we will delve into the various aspects of O-notation to develop a better understanding of how to analyze algorithm complexity.

Big O, Omega and Theta: an overview of the different notations

The O notation is a powerful tool for analyzing algorithm complexity, but it goes beyond the classic Big O notation. In addition to "O", there are also "Ω" (omega) and "Θ" (theta), which describe different aspects of the runtime complexity of an algorithm.

1. Big O (O-Notation): The Big O notation specifies the upper bound of the runtime complexity. It describes how the runtime of the algorithm develops in the worst case. For example, if an algorithm is classified as O(n), this means that the runtime grows linearly with the size of the input.
2. Omega (Ω-notation): The omega notation represents the lower bound of the runtime complexity. It describes how well an algorithm performs in a best-case scenario. If an algorithm is classified as Ω(n²), this means that its runtime grows at least quadratically with the input size.
3. Theta (Θ-Notation): The theta notation is the exact bound and indicates that the running time of an algorithm lies within a certain range. If an algorithm is classified as Θ(n), this means that its runtime grows linearly with the input size, and there is an upper and lower bound that limits the growth.

The choice between these different notations depends on the type of analysis you want to perform. Usually, developers focus on the Big-O notation as it represents the worst-case scenario and is most commonly used to evaluate algorithms. Omega notation helps to understand the best-case scenario, while theta notation allows for a more precise and limited analysis. Knowing and applying these different notations allows developers to make informed decisions when selecting and optimizing algorithms. In the following subtitles, we will dive deeper into the analysis of algorithms and learn about practical applications of these notations.

Best case, worst case and average case: analysis of algorithm behavior

The analysis of algorithm behavior is an important step in the development of efficient software. We often consider three different scenarios: the best case, the worst case and the average case.

1. Best Case: The best case describes the most favorable scenario in which an algorithm has the shortest runtime. This occurs when everything runs smoothly and the algorithm can complete its task with minimal effort. The best-case analysis helps to recognize the potential of an algorithm when the input is already available in optimal form.
2. Worst Case: The worst case represents the most unfavorable scenario in which an algorithm reaches the maximum runtime. This can occur if the input is particularly unfavorable or if the algorithm works under unfavorable conditions. The worst-case analysis is important to ensure that an algorithm never takes an unacceptably long time.
3. Average Case: The average case considers the average runtime of an algorithm over all possible input data. This case is often the most complex to analyze as it depends on the distribution of the input data. The average case analysis is useful to have realistic expectations of the performance of an algorithm.

The choice between these scenarios depends on the requirements and the application domain. In critical systems where fast response times are crucial, worst-case analysis is paramount to ensure that the algorithm performs acceptably under all circumstances. In other cases, where the input data is randomly distributed, average-case analysis can provide better insight into expected performance. The combination of best case, worst case and average case analysis allows developers to make informed decisions when selecting and optimizing algorithms and ensure that their software performs efficiently and reliably in different situations.

O-notation in practice: application examples and areas of use

O-notation is not just a theoretical concept, but an extremely practical tool in the world of software development and computer science. It makes it possible to systematically evaluate the runtime complexity of algorithms and find the best solutions for specific tasks. Here are some examples of applications and areas of use for O-notation:

1. Algorithm comparisons: O-notation makes it easier to compare algorithms for solving the same problem. Developers can analyze the runtime complexity and select the most efficient algorithm for their specific application.
2. Optimization of code: By understanding O-notation, developers can optimize their code to ensure it works on large amounts of data in an acceptable amount of time. They can identify and improve inefficient parts of the code.
3. Hardware selection: When developing applications for specific hardware platforms, it is important to know how different algorithms affect resource utilization. The O-notation helps to select algorithms that fit the hardware limitations.
4. Suchalgorithmen: O-notation is particularly relevant when implementing search algorithms, sorting algorithms and database queries. It helps to optimize the speed of search processes and minimize response times.
5. Game development: In game development, especially for real-time and 3D games, runtime optimization is crucial. Developers use O-notation to ensure that games run smoothly on different platforms.

O-notation is a powerful tool that enables developers to code more efficiently, conserve resources and create better user experiences. It is an essential part of any developer's toolbox and is used in almost all areas of computer science to develop powerful software solutions.