Entschlüsseln der Magie der Mathematik: Eine Reise durch Mathematische Zeichen und Symbole
Veröffentlicht am
Mathematik ist eine Disziplin der Wissenschaft, die sich mit der Untersuchung von Zahlen, Strukturen, Mustern und Verhältnissen befasst. Sie ist eine der ältesten und grundlegendsten Wissenschaften und spielt eine entscheidende Rolle in nahezu allen anderen Bereichen des Wissens und der Anwendung, einschließlich Naturwissenschaften, Ingenieurwissenschaften, Wirtschaft, Informatik und vielen anderen.
Die Mathematik umfasst verschiedene Bereiche, darunter:
- Arithmetik: Dieser Bereich befasst sich mit grundlegenden mathematischen Operationen wie Addition, Subtraktion, Multiplikation und Division. Es ist die Basis für alle weiteren mathematischen Studien.
- Algebra: Algebra beschäftigt sich mit dem Umgang mit Unbekannten und Variablen in Gleichungen und Ungleichungen. Es ermöglicht die Lösung komplexer mathematischer Probleme. (Nicht zu verwechseln mit Lineare Algebra)
- Geometrie: Geometrie untersucht die Eigenschaften von Formen, Größen und Abständen. Sie beschäftigt sich mit Figuren wie Linien, Kreisen, Dreiecken und vielem mehr.
- Analysis: Die Analysis (auch Infinitesimalrechnung genannt) ist ein Bereich der Mathematik, der sich mit Grenzwerten, Ableitungen und Integralen beschäftigt. Sie ist fundamental für das Verständnis von Veränderung und Kontinuität.
- Statistik: Die Statistik beschäftigt sich mit der Sammlung, Analyse und Interpretation von Daten. Sie spielt eine wichtige Rolle in der empirischen Forschung und in Entscheidungsprozessen.
- Wahrscheinlichkeitstheorie: Dieser Bereich der Mathematik untersucht zufällige Ereignisse und deren Wahrscheinlichkeiten. Sie findet Anwendung in der Statistik, der Finanzmathematik und vielen anderen Bereichen.
- Diskrete Mathematik: Dieser Bereich beschäftigt sich mit diskreten Strukturen, wie beispielsweise Graphentheorie und Zahlentheorie. Er findet Anwendung in der Informatik und der Kryptographie.
Mathematik ist nicht nur eine theoretische Disziplin, sondern hat auch praktische Anwendungen in verschiedenen Bereichen des täglichen Lebens. Sie ist ein mächtiges Werkzeug zur Problemlösung und zur Modellierung von Phänomenen in der realen Welt.
Mathematik Zeichen
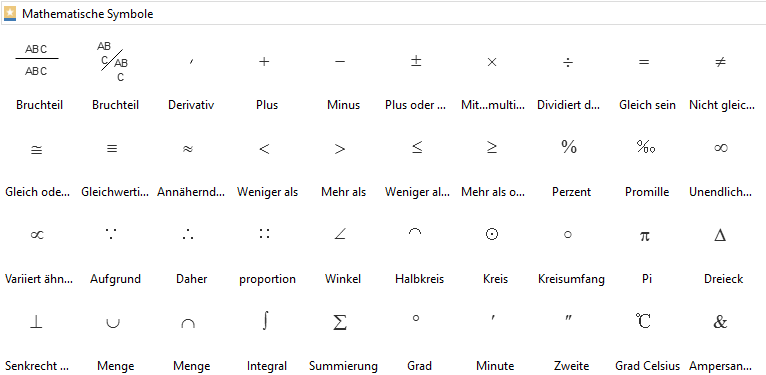
Es gibt eine große Anzahl von mathematischen Zeichen und Symbolen, die in der Mathematik verwendet werden. Es ist schwer, eine genaue Anzahl festzulegen, da neue Symbole entwickelt werden können und einige Symbole in verschiedenen Bereichen der Mathematik unterschiedliche Bedeutungen haben können. Hier sind jedoch einige der häufigsten mathematischen Symbole:
- Zahlen: Zahlen wie 0, 1, 2, 3, ... sind grundlegende mathematische Symbole.
- Grundrechenzeichen: Symbole wie + (Addition), - (Subtraktion), * (Multiplikation) und / (Division) werden in arithmetischen Operationen verwendet.
- Griechische Buchstaben: Griechische Buchstaben wie α (Alpha), β (Beta), γ (Gamma) und δ (Delta) werden in der Mathematik oft als Variablen oder Konstanten verwendet.
- Algebraische Symbole: Symbole wie x, y, z werden häufig als Variablen in algebraischen Gleichungen verwendet.
- Relationale Symbole: Symbole wie = (Gleichheit), ≠ (Ungleichheit), < (kleiner als), > (größer als), ≤ (kleiner oder gleich) und ≥ (größer oder gleich) werden verwendet, um Beziehungen zwischen Zahlen oder Ausdrücken auszudrücken.
- Operatoren: Symbole wie ∑ (Summe), ∫ (Integral), ∆ (Differenz) und √ (Quadratwurzel) werden verwendet, um mathematische Operationen darzustellen.
- Mengensymbole: Symbole wie ∈ (Element von), ∪ (Vereinigung), ∩ (Durchschnitt) und ⊆ (Teilmenge) werden in der Mengenlehre verwendet.
- Trigonometrische Symbole: Symbole wie sin (Sinus), cos (Kosinus) und tan (Tangens) werden in der Trigonometrie verwendet.
- Logarithmische Symbole: Symbole wie log (Logarithmus) und ln (natürlicher Logarithmus) werden in der Analysis verwendet.
- Spezielle mathematische Symbole: Es gibt auch viele spezielle Symbole für mathematische Konzepte wie ∞ (Unendlichkeit), π (Pi), e (Eulersche Zahl) und i (imaginäre Einheit).
- Integrationszeichen (∫): Steht für die Integration, das Umkehren der Ableitung, in der Analysis.
- Quadratwurzel (√): Zeigt die positive Quadratwurzel einer Zahl an.
- Kubikwurzel (∛): Zeigt die positive Kubikwurzel einer Zahl an.
- Element-von-Symbol (∈): Wird verwendet, um anzuzeigen, dass ein Element zu einer bestimmten Menge gehört.
- Vereinigungszeichen (∪): Stellt die Vereinigung von Mengen dar, d.h., alle Elemente, die in mindestens einer der Mengen enthalten sind.
- Durchschnittszeichen (∩): Zeigt den Durchschnitt von Mengen an, d.h., die Elemente, die in allen Mengen enthalten sind.
- Teilmenge-Symbol (⊆): Wird verwendet, um anzuzeigen, dass eine Menge eine Teilmenge einer anderen Menge ist.
- Gleichheitszeichen (=): Zeigt an, dass zwei Ausdrücke oder Werte gleich sind.
- Ungleichheitszeichen (≠): Zeigt an, dass zwei Ausdrücke oder Werte nicht gleich sind.
- Kleiner-als-Zeichen (<) und Größer-als-Zeichen (>): Zeigen an, dass ein Wert kleiner bzw. größer als ein anderer Wert ist.
- Kleiner-oder-gleich-als-Zeichen (≤) und Größer-oder-gleich-als-Zeichen (≥): Zeigen an, dass ein Wert kleiner oder gleich bzw. größer oder gleich einem anderen Wert ist.
- Sinus (sin), Kosinus (cos) und Tangens (tan): Trigonometrische Funktionen, die in der Geometrie und Trigonometrie verwendet werden.
- Logarithmus (log) und natürlicher Logarithmus (ln): Mathematische Funktionen zur Berechnung von Exponenten und Potenzen.
- Unendlichkeit (∞): Ein mathematisches Konzept, das eine unendliche Größe oder Menge repräsentiert.
- Pi (π): Eine mathematische Konstante, die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser darstellt.
- Eulersche Zahl (e): Eine wichtige mathematische Konstante, die in der Analysis und der exponentiellen Funktion vorkommt.
- Imaginäre Einheit (i): Eine mathematische Einheit, die in der komplexen Zahlentheorie verwendet wird, um komplexe Zahlen darzustellen.
Diese Liste erhebt keinen Anspruch auf Vollständigkeit, da es viele weitere mathematische Symbole und Konzepte gibt. Mathematik ist eine äußerst vielseitige und breite Disziplin, und die Verwendung von Symbolen kann je nach mathematischem Bereich variieren.








