O-Notation: Analyse der Algorithmuskomplexität

Veröffentlicht am

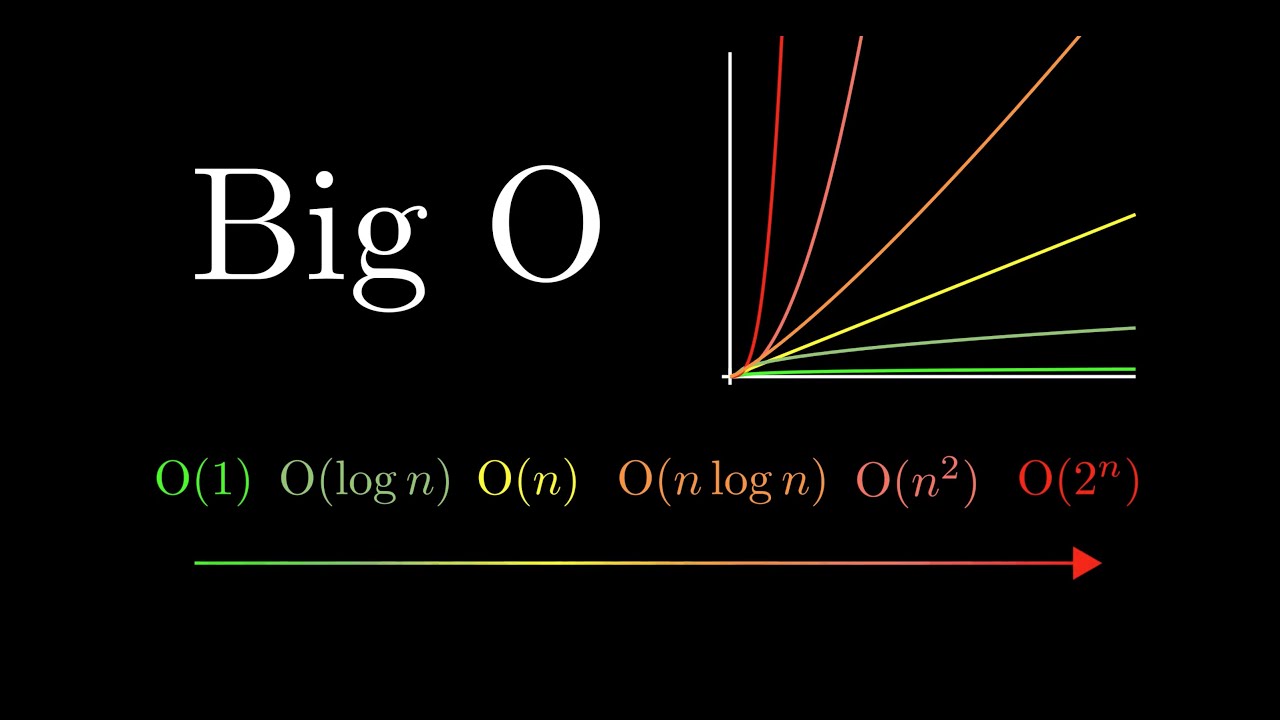
Blog image

Das könnte Sie auch interessieren

Hauptbild

Maschinencode: Die Sprache der Computer

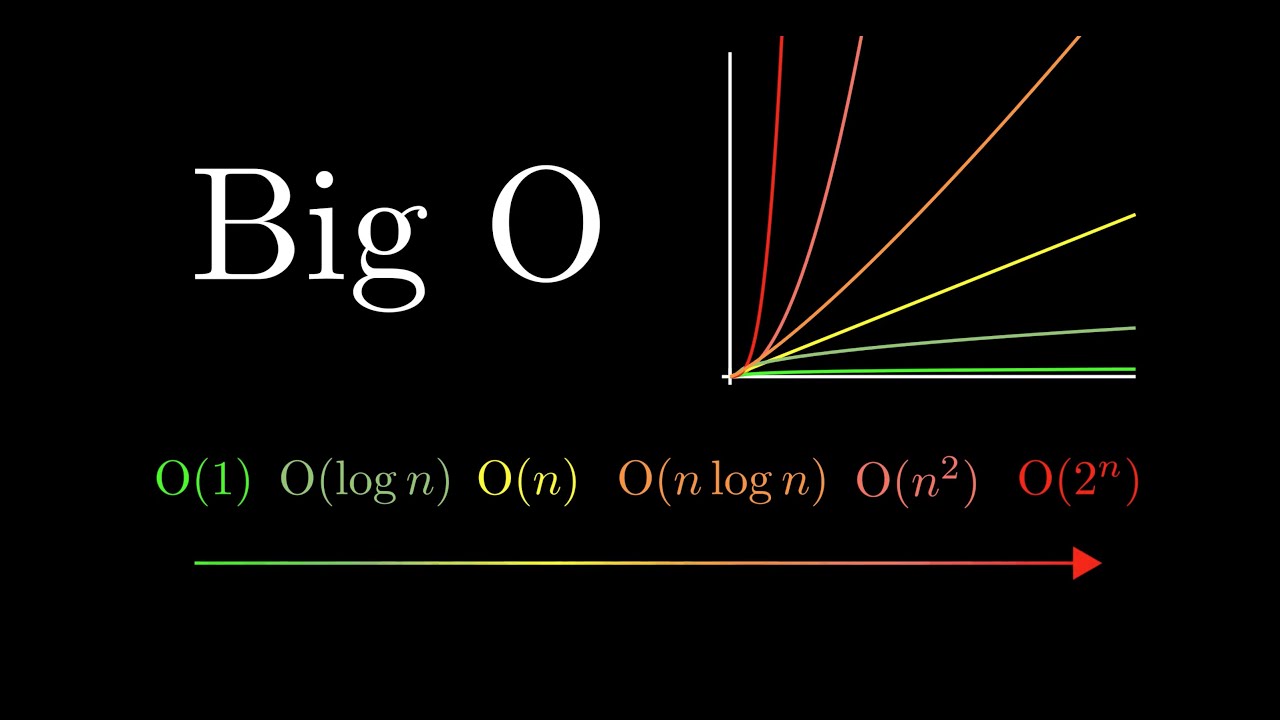
RemoteScout24 · Veröffentlicht am 2023-09-19 17:59:01.0

Hauptbild

Assembler-Sprache: Die niedrige Ebene der Programmierung

RemoteScout24 · Veröffentlicht am 2023-09-18 17:59:01.0

Hauptbild

Maschinenbau: Die Welt der mechanischen Innovation

RemoteScout24 · Veröffentlicht am 2023-09-18 17:59:01.0

Hauptbild

Elektronik: Die Welt der elektronischen Innovation

RemoteScout24 · Veröffentlicht am 2023-09-17 17:59:01.0